《分一分（一）》

执教教师：赵砚     长春市第一实验银河小学

【执教教师简介】

赵砚，吉林省长春市第一实验银河小学数学教师，毕业于北华大学小学教育专业，2006年踏入工作岗位。2012-2015年在东北师范大学教育学部初等教育学院学习，2015年获得教育硕士学位。从事小学数学教学以来，虚心求教，大胆尝试，追求“把数学画出来”的课堂。尊重学生的学习起点，努力做一名受学生喜爱的老师。

【教学内容】

新世纪小学数学（北师大版）三年级下册67页。

【教材分析】

教材给出的是学生熟悉的数学情境：一个苹果平均分给两个人，每个人分得半个苹果，讨论用什么数字符号表示“一半”。这个过程中一方面让学生意识到原来的数字符号不能表示新的数量，要用新的符号表示出“一半”；另一方面让学生参与创造，感受表示“一半”的方法，进而让学生在操作和描述活动过程中理解分数所表示的符号意义，并会认、会读、会写分数，认识分数的各部分名称。从符号意识角度分析，本课要让学生理解分数与自然数具有相同的符号意义，也就是用来表示具体数量，是对具体数量的符号化表示。有些量可以用自然数来表示，而分数就是用来表示无法用自然数度量的量，是通过分割产生的新的数，分数正是能够精确地表示这类数而引入的数学符号。

【学生分析】

学生正式学习分数以前，已经理解“平均分”。“二分之一”“三分之一”等语句表达已经出现在他们的口头语言中，只是还不曾想过要用数字符号来表示它们，最先认识分数也是从平均分物体入手。此阶段是学生由图形语言到符号语言表达的转化。因此，教材主要从学生所熟悉并感兴趣的生活经验出发，利用直观的方式，使学生通过折一折、涂一涂等动手操作的活动，逐渐形成分数的符号化表象，建立对分数的符号化形式的理解，而再进一步理解分数的意义，并将意义与符号统一。

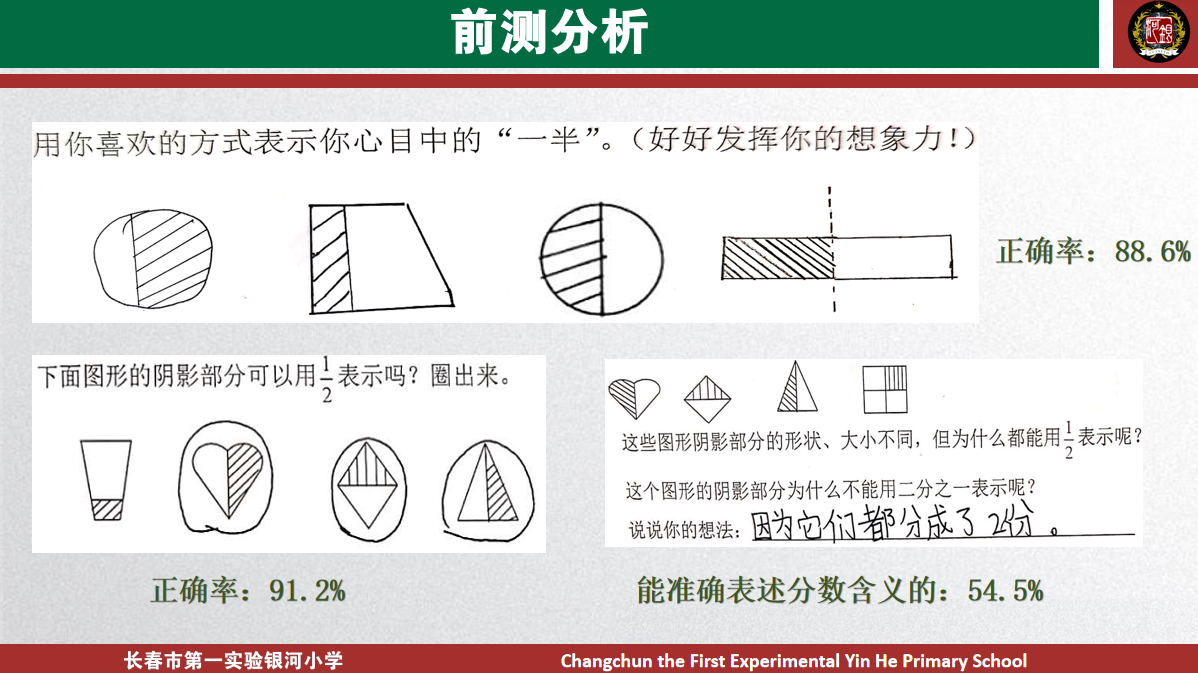
从前测看，学生对分数有一定的了解。所以课堂中要不断以学促教，让学生由自然结构向知识结构转化。利用几何直观将学生已有的经验与知识，通过适当的操作活动展示出来，将数字符号用自己理解的图画体现出来，不仅拉近了数学符号与学习情境的距离，更让学生的思考有的放矢，有参照、有对比，这样才能建立比较清晰、准确的认识，才能从本质上理解数字符号的意义。

【学习目标】

1. 结合直观操作，初步理解分数的意义，体会分数产生的必要性，能读、写分数，知道分数各部分名称。

2. 探索分数单位的产生，感悟分数的符号本质。经历分数单位累加的过程；体验度量中“标准”的重要作用。渗透符号化思想。

3. 理解分数的符号含义，学会用数学思维来思考问题，初步感受用数学符号表示数量的价值。

【教学过程】

一、对比引新，初步感知“一半”的符号意义。

1. 初步感悟“整个”的与“半个”的符号区别。

（1）（出示2个苹果的学具贴）同学们，请看这是什么？

2个苹果，可以用“2个”记录，如果把2个苹果平均分给2位同学，怎样分呢？

预设：平均分，每人分1个。

（2）如果再把1个苹果平均分给2位同学呢？怎么分？能用老师的学具演示一下吗？（学生演示）这样来看，每位同学得到了几个苹果？

预设：半个，一半。（板书）

（3）之前我们可以用2个、1个这样的数来记录数量，那么这个“半个”、“一半”怎么记录呢？这节课就让我们一边分一边研究。（板书：分一分（一））

2. 探究“一半”，抽象“一半”的符号意义。

（1）同学们提到“一半”，平时大家用过这个词吗？我们平时也经常用这个词来表示物体的数量。

那么请大家在白纸上画出一个图形，并用阴影表示出这个图形的“一半”。

（2）（学生创作，教师巡视，选取代表性作品贴于黑板上）同学们，大家请仔细观察，阴影部分都可以表示出这个图形的“一半”吗？

学生质疑，最终明确想要找到“一半”必须建立在平均分基础上。

（3）明确“一半”与平均分成2份表示其中1份的联系。

同学们的作品，图形形状、大小都不一样，为什么阴影部分都可以表示出这个图形的“一半”？

小结：只要把一个图形平均分成了2份，那么其中的一份就是它的“一半”。

【设计意图】帮助学生感悟“整个”与“一半”的符号特征，为接下来理解分数单位积累数学活动经验。当不能用自然数的符号来表示，需要引入一种新的符号，在此制造矛盾冲突，激发学生的探索欲望。

二、直观感知，探究二分之一的符号本质。

1.借助直观，感悟“二分之一”的符号本质。

（1）我们看到之前用2、1这样的数来记录苹果的数量，如果也想用数来表示出“一半”这样的数量，该用哪个数呢？大家想一想这个数要体现出什么呢？

预设：这个数要体现出平均分2份和其中的1份。

（2）知道这个数是什么样的数吗？对，正如同学们所说，这个数就是“二分之一”（板书）

2.借助素材，理解“二分之一”符号本质。

（1）“二分之一”这个数与之前的数有很大不同，用了两个数来表示“一半”，为什么要用到两个呢？这两个数用来表示什么呢？

（2）这个分数表示出了表示平均分的份数，“1”表示2份中的那1份。

根据学生回答，将平均分的“2份”与分数中的“2”勾连起来，将其中的“1份”与分数中的“1”勾连起来。

总结：“2”和“1”共同发挥作用就把像这样“一半”的数量表示出来了。

3.对比分析，深化“二分之一”的符号本质。

（1）老师给每个同学也发了一些图形，请你用阴影表示出这些图形的二分之一。教师巡视，将有代表性的作品贴于黑板上。

（2）请同学们观察黑板上的作品，每个图形的阴影部分都可以用“二分之一”表示吗？（找到不同的）这几个阴影都不一样，都能用二分之一表示吗？为什么

预设：都是把“正方形”平均分成两份，都表示出了其中的一份，就都可以用二分之一来表示。

（3）仔细观察，这些不同的图形，它们的形状、大小、分法都不相同，为什么都可以用二分之一来表示？

小结：只要把一个图形平均分成两份，那么表示其中的一份可以用二分之一来记录。

【设计意图】借助学生的图画作为素材，对学生的直观图画进行分析、对比，进而抽取共同的、本质的符号特征，借助生活情境进一步丰富二分之一的数字符号意义，从而完善二分之一作为数量符号的本质概念。

三、动手操作，构建几分之一的符号理解。

1.折、涂当中构建“几分之一”符号表象。

（1）学生自由表征几分之一。

同学们手中都有一张纸条，想一想，你还能找到这张纸条的几分之一？

出示探究要求：动手折一折、找一找几分之几，并用阴影表示。教师巡视，选取有代表性的作品贴于黑板。

2.借助直观，将不同的分数单位用符号表达。

（1）引导学生观察直观作品，发现不同的分数单位。

从这些作品中你看出了几分之一？说一说你是怎样看出来的？

根据学生的回答将平均分的份数与表示的份数与分数当中的“分子”、“分母”勾连起来。

（2）讨论分法不同但表示分数含义相同的作品。加深分数含义的理解。

预设：这几个四分之一怎么长得不一样？都能表示四分之一吗？只要平均分，并表示其中的一份，就都可以用几分之一来表示。

3.初步感悟分数单位的符号意义。

引导观察，为什么涂阴影的部分都是1份，但写出来的分数却不一样呢？

预设：因为平均分成的份数不相同，虽然同样是取出一份，但表示的分数也不一样。

【设计意图】利用学生创作的几分之一图片作为素材，进一步巩固学生对于几分之一的符号理解。同时初步感知了不同的分数单位，理解数字符号中分子、分母以及分数线在具体情境中的含义，将数字符号与具体情境关联，达到了对符号各个部分的理解。

四、在“涂”中构建几分之几的符号理解。

1.涂出几分之几，感悟几分之几的符号意义。

教师手势指引：在这里再涂一份，阴影部分可以怎么表示？再涂一份……

你是怎样看出来这是几分之几的？学生语言表达几分之几的形成过程。

2.经历分数单位累加的过程，构建与数学符号的关联。

（1）操作中感悟几分之几的符号意义。

请一位同学说出一个分数，这个分数能用黑板上的作品涂出来。

请同学们想一想，这个分数可以在哪个作品上涂出来？为什么？

（2）操作经历分数单位的累加，深化“几分之几”的符号理解。

请同学们利用自己的作品也涂出一个分数，并且与同桌讲一讲。

3.介绍分数各部分名称并构建各部分的符号理解。

我们已经创作了这么多分数，让我们一起读一读。

介绍：每个分数由三部分组成，中间这条线叫分数线，分数线下面的数叫“分母”上面的数叫“分子”。

请同学们说一说，通过刚才的学习你发现分母和分子都发挥了什么样的作用？

小结：分母表示出了平均分的份数，分子表示出其中的几份。

【设计意图】学生在操作中画出了更小的分数单位，初步探索了在相同整体中平均分的份数与一份大小的关系。通过涂一涂找一找，经历了分数单位产生和累加的过程，感知分数是由若干个分数单位累加而成。借助几何直观把数与图对应起来，进一步感知分数的符号价值。

五、全课小结，分享收获。

同学们，以前我们知道可以用2、1这样的数来表示物体的数量，今天通过学习我们知道了，物体的数量也可以用分数来表示。说一说你有哪些收获？

预设：分数是“平均分”分出来的，先平均分成几份，再数一数有几个几分之一。是几分之一、几分之一数出来的，是几分之一的累加，原来数都是数出来的！原来比1小的数量也可以用数来表示。

【思考在延伸】

本节课是分数的初步认识，包含了分数的两方面意义：一是量的意义，另一个是率的意义。从整数到分数是数概念的一次数量符号的扩充。应该让学生理解分数与自然数具有相同意义，也就是表示一种量，那么在教学中是否应该量在前率在后，两个符号意义谁前谁后？如何做到统一或齐头并进？

三年级学生虽然抽象思维的水平有所发展，但还是以形象思维为主，因此利用已有的经验与知识，通过适当的操作活动，利用几何直观，建立对分数这一符号清晰、准确的认识。期间也利用了大量的学生创作的素材去对比、分析，构建对二分之一的理解。接着利用学作品和教材中的素材，对比大小、形状不同的涂色图形，这样为抽象概括提供支撑，有助于学生对二分之一的符号本质的提取。但从设计整体上来看这样的设计却更加偏重于率的感知，缺少了对量的丰富。很多教师也有这样的困惑，起初以量引入，教着教着就变成“率”了。如何让学生以“量”的角度对分数的符号意义有更加丰富的认识？这便是我们对这节课的困惑。